How To Find Maximum Slope Of Tangent Line

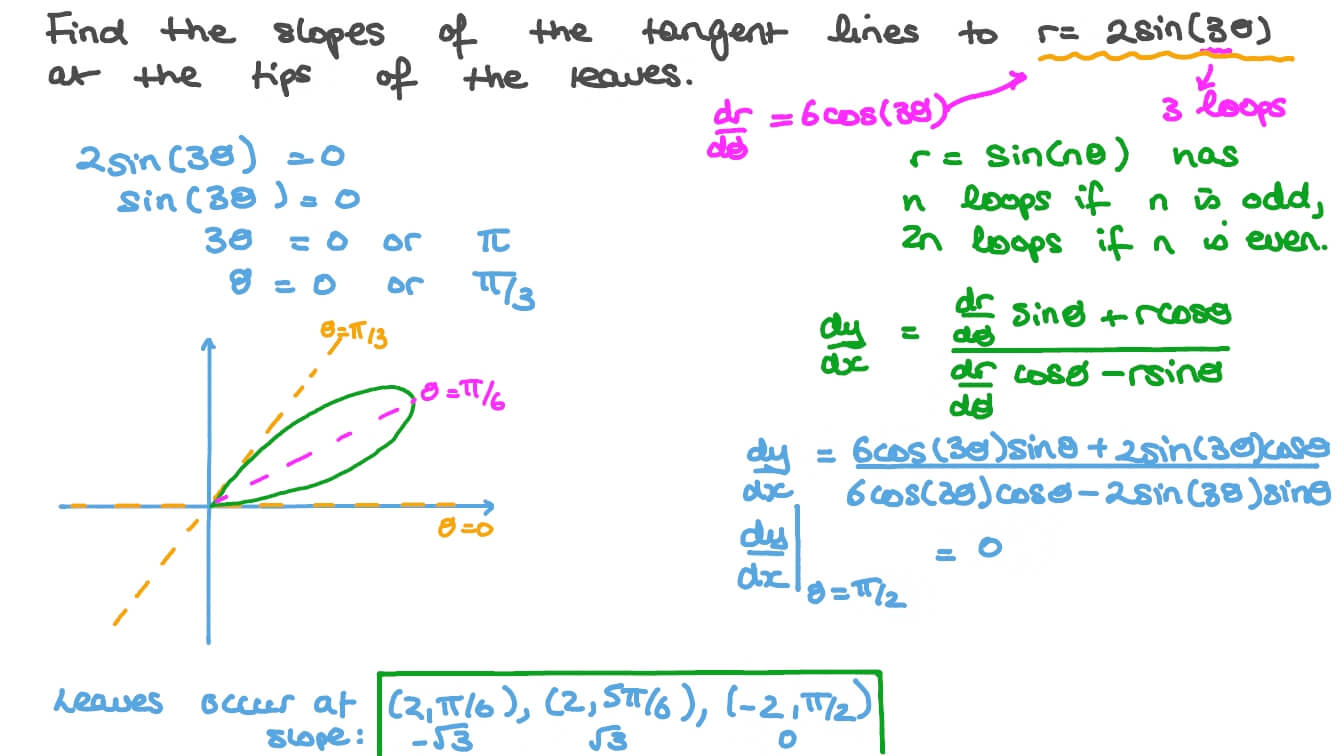
So for this problem, we want to find where our graph of y is equal to one over one. So we can think of this as a maximizing problem. And essentially, we're going to be able to find the formula that we're trying to maximize by finding the first derivative of our equation. And we know that that's going to give us the equation of our slope. So when we find this first derivative, we're going to end up, we can actually write this as, ah one plus X squared to the negative one power. So using the power rule, this will be negative one plus x squared times two x, which will just simplify to negative to X over one plus X squared.

And we know that since we're trying to maximize this equation, we're going to take the derivative of this and said that equal to zero. Times I did not make her unchanged, which is one plus x squared. And we're going to subtract the numerator unchanged times the derivative of the denominator. I'm so the derivative of one plus x squared.

Um, and this should have been to the negative to power. So should have been squared here is going to end up being too times what was on the inside one plus X squared to the two minus one power times the derivative of our inside here. So times to X and this is all divided by our denominator squared. So that'll end up being one plus X squared to the fourth power and we can see that we're going to be able to cancel out some of these one plus X squared terms. So we have one here in numerator on this one was squared, so it's not going to become the first power and the denominator. We have a cute And since we're trying to maximize us, we're just going to set this equal to zero.

And so when we do that and simplify our terms, we're going to end up finding our new writer will become six X squared minus two is your equal to zero. So when we solve for X, we at X equal to either the positive or negative square root of 1/3. And from here, we need to determine whether be positive or negative square root is going to give us our maximum.

Essentially, we're just going to plug in X equal to the positive square root of 1/3 and negative square to 1/3 into our Y prime function. I'm so if we plug in X is equal to the positive square root of 1/3 we end up finding that Y prime is equal to your negative nine over to Times Square to six. Um, And if we plug in X is equal to the negative square root of 1/3 we get why prime is equal to positive nine over to Times Square to six.

So that tells us that, uh, the maximum slope is going to be right here at X is equal to negative 1/3. You can determine the slope of a tangent line at any point on a function using calculus. The calculus approach requires taking the derivative of the function from which the tangent line originates.

By definition, the derivative of a function at any given point is equal to the slope of the tangent at that point. This value is also sometimes described as the instantaneous rate of change of the function. Although calculus has a reputation for being difficult, you can find the derivative to most simple algebraic functions quickly. "corrected values" of the QT interval were provided as the difference between automated and manual QT interval. Figures 1 and 2 show automated measurement of the QT interval by the tangent and differential threshold methods, respectively. In the tangent method, the maximum slope of the descending limb of the T wave is identified from the maximum negative value of the differentiated waveform.

In terms of the W function, which was developed specifically to solve equations of this type. While there does exist a general algebraic method for computing derivatives, there is no general algebraic method for solving equations. Even for polynomials, it is known that there can be no generally useful algebraic method of finding roots (i.e., there can be no analog of the quadratic formula) for degree five or above. This is why it is often necessary to resort to numerical approximation methods to solve algebraic equations. Tangent lines, well it's an important topic.

In this episode, we've covered finding the slopes of curves at particular spots. We've covered finding the equation of tangent lines, at those particular spots. You'll often see questions on the AP test where they're going to ask you to find the equation of a tangent line at a curve, or even just the slope at a particular spot. They're really common on the multiple choice section. You may or may not see an optimization problem in the free response section. The derivative of a function has many applications to problems in calculus.

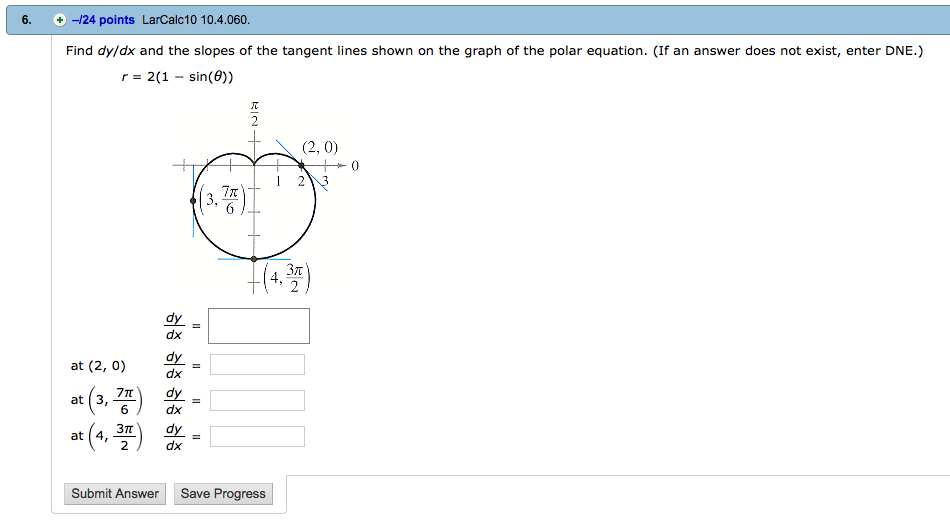
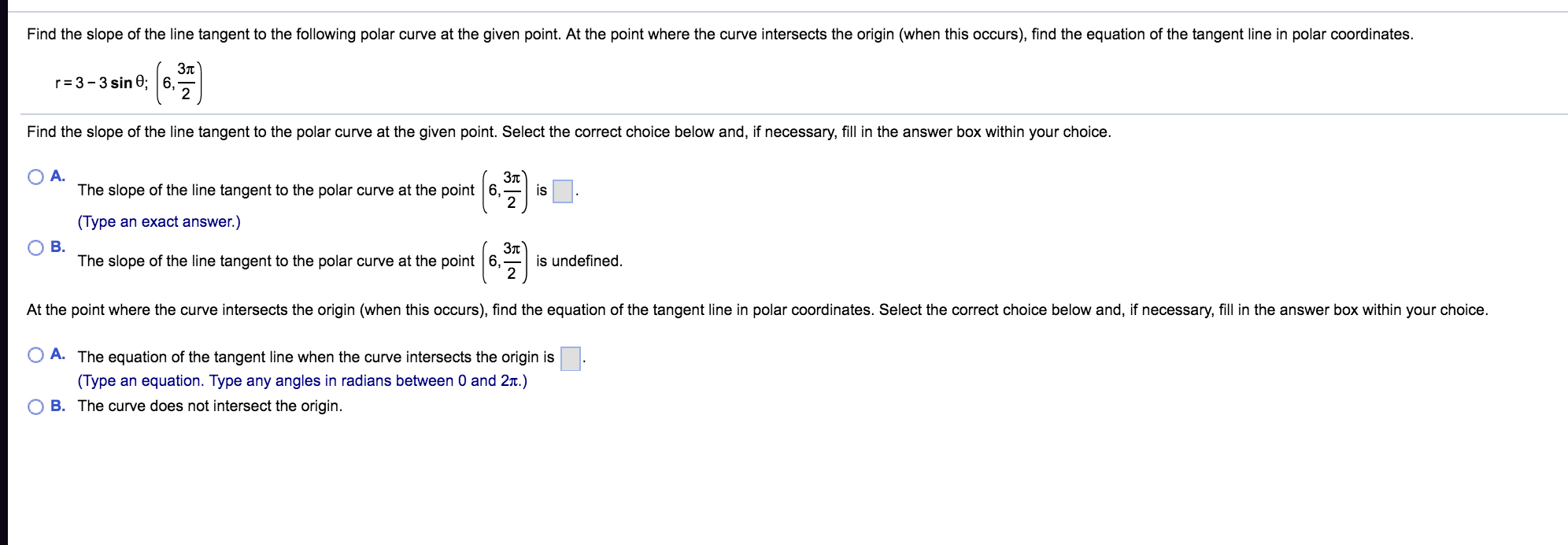
It may be used in curve sketching; solving maximum and minimum problems; solving distance; velocity, and acceleration problems; solving related rate problems; and approximating function values. Since the derivative is zero or undefined at both local maximum and local minimum points, we need a way to determine which, if either, actually occurs. Using differential calculus, we can determine the limit, or the value that Δy/Δx approaches as Δy and Δx get closer to zero; it follows that this limit is the exact slope of the tangent. If y is dependent on x, then it is sufficient to take the limit where only Δx approaches zero. Therefore, the slope of the tangent is the limit of Δy/Δx as Δx approaches zero, or dy/dx.

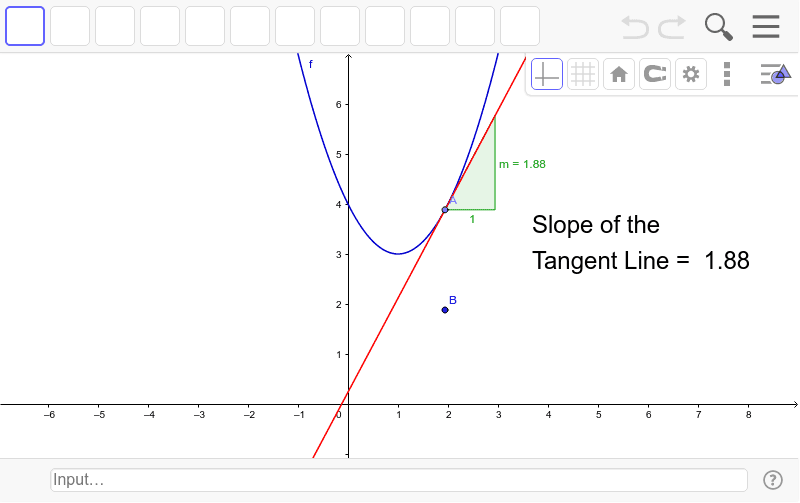
The concept of a slope is central to differential calculus. For non-linear functions, the rate of change varies along the curve. The derivative of the function at a point is the slope of the line tangent to the curve at the point, and is thus equal to the rate of change of the function at that point.

If $(x,f)$ is a point where $f$ reaches a local maximum or minimum, and if the derivative of $f$ exists at $x$, then the graph has a tangent line and the tangent line must be horizontal. This is important enough to state as a theorem, though we will not prove it. As a generalization of this practical description, the mathematics of differential calculus defines the slope of a curve at a point as the slope of the tangent line at that point. When the curve is given by a series of points in a diagram or in a list of the coordinates of points, the slope may be calculated not at a point but between any two given points. This process is sometimes used to find the maximum or minimum values of a curved function, since the tangent line slope will be zero at such points. Has a local maximum at the point where the graph changes from increasing to decreasing.

The graph has a local minimum at the point where the graph changes from decreasing to increasing. Again, at this point the tangent has zero slope. How tangent lines are a limit of secant lines, and where the derivative and rate of change fit into all this. Unlike a straight line, a curve's slope constantly changes as you move along the graph. To find the equation for the tangent, you'll need to know how to take the derivative of the original equation. Well this is a topic from fairly early on in the year just after you learnt how to do derivatives.

What this topic does is help you find the minimums and maximum of curves, and you can also find lines that are a tangent to a curve at any spot. So we're going to begin by doing a little bit of basic review. We'll go on to a few practise problems and then we'll go to some applications. Applications involving optimization problems. Calculus equations that seek to determine the maximum or minimum value for a given parameter are called optimization problems. Learn about optimization problems through real-world examples/explanations and how to use the six-step method to solve optimization problems in calculus.

In addition to finding the area under a parametric curve, we sometimes need to find the arc length of a parametric curve. In the case of a line segment, arc length is the same as the distance between the endpoints. If a particle travels from point \(A\) to point \(B\) along a curve, then the distance that particle travels is the arc length. To develop a formula for arc length, we start with an approximation by line segments as shown in the following graph. \(t\) \(x\) \(y\) \(\dfrac\) 0 5 \(π\) −5 0 \(\dfrac\) 0 −5 \(2π\) 5 0 These points correspond to the sides, top, and bottom of the circle that is represented by the parametric equations .

On the left and right edges of the circle, the derivative is undefined, and on the top and bottom, the derivative equals zero. A tangent is drawn from that point, and the distance from the point where the tangent crosses the baseline to the start of the QRS complex is measured. For any constant C, we see that all the tangent line segments along this line have the same slope, no matter what the value of the independent variable, say t. Another way to look at this is to realize that we can generate infinitely many solutions by taking any one solution and translating its graph left or right.

Even when we can't solve an equation, an analysis of its slope field can be very instructive. However, such a graphical analysis may miss certain important features of the integral curves, such as vertical asymptotes. To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope. Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph.

For each possible extreme point, plug the x-coordinate a into f''. If f'' is positive, there is a local minimum at a. If f'' is negative, there is a local maximum. If f'' is 0, there is an inflection point, not an extreme point.

So our two numbers are square roots of 612 and square root of 612. "Oh! No they're back." Find the maximum volume of an open top box that can be made of 8x14 sheet. These things were probably your nemesis in pre-calc.

Most pre-calc courses of these days will have some of these on there. But in pre-calc you had to find the solution by using graphing calculator. Now that we're using calculus, you've been liberated from that calculator. Local maximum and minimum points are quite distinctive on the graph of a function, and are therefore useful in understanding the shape of the graph.

In many applied problems we want to find the largest or smallest value that a function achieves and so identifying maximum and minimum points will be useful for applied problems as well. Some examples of local maximum and minimum points are shown in figure 5.1.1. In reality there probably won't be 15 cm3 more air in the balloon after an hour. The rate at which the volume is changing is generally not constant so we can't make any real determination as to what the volume will be in another hour.

Many common questions asked on the AP Calculus Exams involve finding the equation of a line tangent to a curve at a point. If we are adept at quickly taking derivatives of functions, then 90 percent of the work for these types of problems is done. Everything else comes down to quick algebra. Calculate the derivative \(\dfrac\) for each of the following parametrically defined plane curves, and locate any critical points on their respective graphs. At the point P means the slope of the tangent at the point P.

We need to find this slope to solve many applications since it tells us the rate of change at a particular instant. So in this sense, calling it a tangent line seems reasonable. However, the red line also intersects the curve in two places, which suggests the reverse if we adhere to the old geometric definition of a tangent line. Knowing the slopes of tangent lines at various points on the graph of a function can help one better understand the graph of the overall function.

Let us look at a max problem in a different environment. However, first you attempt a solution using your knowledge of calculus. Suppose your company wishes to make packaging boxes from 32 inch square pieces of metal. You are requested to design the box with maximum volume by cutting squares out of the corners. What is the equation you will use to maximize? (Remember, you are saving the company money!) 3.

That is, explain your use of the calculus. The answer is yes, if you can write the equation for the strength and then find a root of its derivative. Let us first examine the problem with the aid of the Geometer's Sketch Pad. Here you will see a graph produced of the strength equation and locate its maximum. Later we will look at the graph of the first derivative and note its root. Click on the word beam to access the sketch.

Use the available log sizer, wood constant sizer , and animation feature to determine the strength of some beams. The derivative of a function at a point is the slope of the tangent line at this point. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. Because the slopes of perpendicular lines are negative reciprocals of one another, the slope of the normal line to the graph of f is −1/ f′. Slope is calculated by finding the ratio of the "vertical change" to the "horizontal change" between two distinct points on a line. Sometimes the ratio is expressed as a quotient ("rise over run"), giving the same number for every two distinct points on the same line.

A line that is decreasing has a negative "rise". The line may be practical - as set by a road surveyor, or in a diagram that models a road or a roof either as a description or as a plan. For the given problem, we want to find the slope of the tangent line to the graph at the given point and then determine an equation of the tangent line. So we see that the slope of the tangent line, This function right here is a negative Acts to the -1. We want to find the slope at three negative one third. Let's briefly look at the velocity problem.

How To Find The Slope Of A Tangent Line Using Limits Many calculus books will treat this as its own problem. We however, like to think of this as a special case of the rate of change problem. In the velocity problem we are given a position function of an object, \(f\left( t \right)\), that gives the position of an object at time \(t\). Then to compute the instantaneous velocity of the object we just need to recall that the velocity is nothing more than the rate at which the position is changing. As with the tangent line problem all that we're going to be able to do at this point is to estimate the rate of change.

So, let's continue with the examples above and think of \(f\left( x \right)\) as something that is changing in time and \(x\) being the time measurement. Again, \(x\) doesn't have to represent time but it will make the explanation a little easier. While we can't compute the instantaneous rate of change at this point we can find the average rate of change.

When studying mathematics functions and methodology of calculation, a good place to start is understanding the significance of one-sided limits and continuity. Learn more about the properties and functions, and study an example of a formula for finding one-sided limits and continuity. Concave up describes a section of a curve if the graph is gradually increasing in slope from left to right. Learn the definition of concave up, how it applies to functions and graphs, and the math behind concavity.